- Fmap
- Setters
- Folds
- Lenses
- Conclusion
- References
Contents
Lenses In Pictures
You should know what a functor is before reading this post. Read this to learn about functors.
Suppose you want to make a game:

data Point = Point { _x, _y :: Double }
data Mario = Mario { _location :: Point }
player1 = Mario (Point 0 0)
Ok, now how would you move this player?
moveX (Mario (Point xpos ypos)) val = Mario (Point (xpos + val) ypos)
Instead, lenses allow you to write something like this:
location.x `over` (+10) $ player1
Or this is the same thing:
over (location . x) (+10) player1
Lenses allow you to selectively modify just a part of your data:
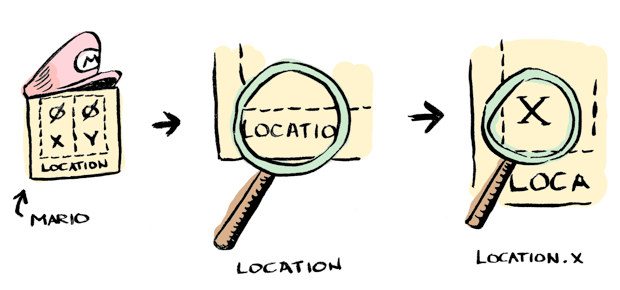
Much clearer! The full example is here.
location is a lens. And x is a lens. Here I composed these lenses together to modify a sub-part of player1.
Fmap
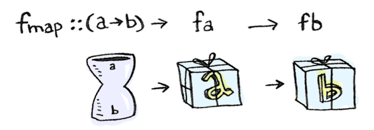
You probably know how fmap works, Doctor Watson (read this if you don't):
Well old chap, what if you have nested functors instead?
You need to use two fmaps!
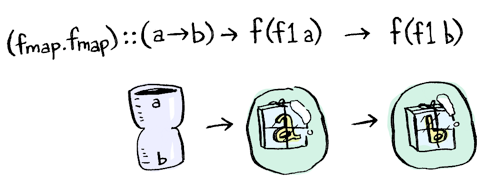
Now, you probably know how function composition works:
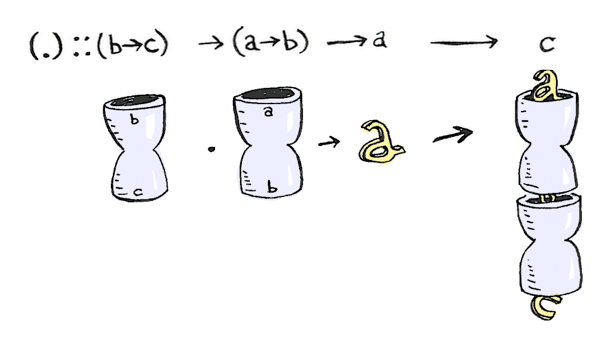
What about function composition composition?
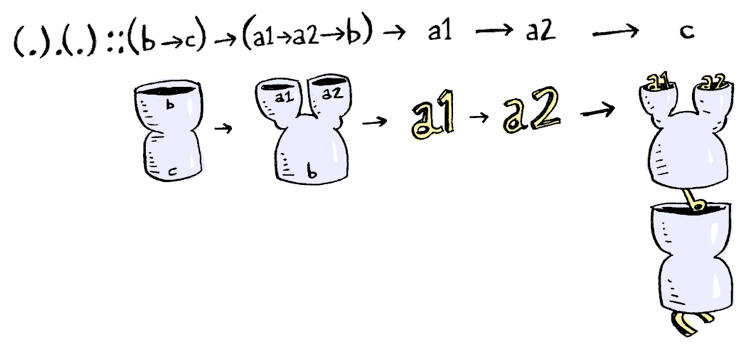
"If you want to do function composition where a function has two arguments", says Sherlock, "you need (.).(.)!"
"That looks like a startled owl", exclaims Watson.
"Indeed. Let's see why this works."
The type signature for function composition is:
(.) :: (b -> c) -> (a -> b) -> (a -> c)
Which looks a heck of a lot like fmap!
fmap :: (a -> b) -> f a -> f b
In fact if you replace a -> with f it's exactly fmap!
And guess what! a -> is a functor! It's defined like this:
instance Functor ((->) r) where
fmap = (.)
So for functions, fmap is just function composition! (.).(.) is the same as fmap . fmap!
(.).(.) :: (b -> c) -> (a1 -> a2 -> b) -> (a1 -> a2 -> c)
fmap . fmap :: (a -> b) -> f (f1 a) -> f (f1 b)
There's a pattern happening here: fmap . fmap and (.) . (.) both allow us to go "one level deeper". In fmap it means going inside one more layer of functors. In function composition your functor is r ->, so it means you can pass in one more argument to your function.

Setters
Suppose you have a function double like so:
double :: Int -> Maybe Int
double x = Just (x * 2)
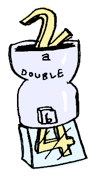
You can apply it to a list with traverse:
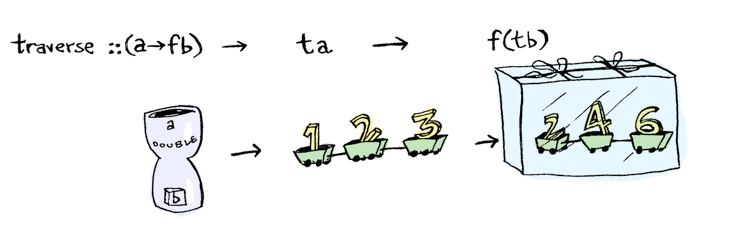
So you pass in a traversable and a function that returns a value wrapped in a functor. You get back a traversable wrapped in that functor. As usual, you can go one level deeper by composing traverse:
traverse :: (a -> m b) -> f a -> m (f b)
traverse.traverse :: (a -> m b) -> f (g a) -> m (f (g b))
traverse is more powerful than fmap though because it can be defined with traverse:
fmapDefault :: Traversable t => (a -> b) -> t a -> t b
fmapDefault f = runIdentity . traverse (Identity . f)
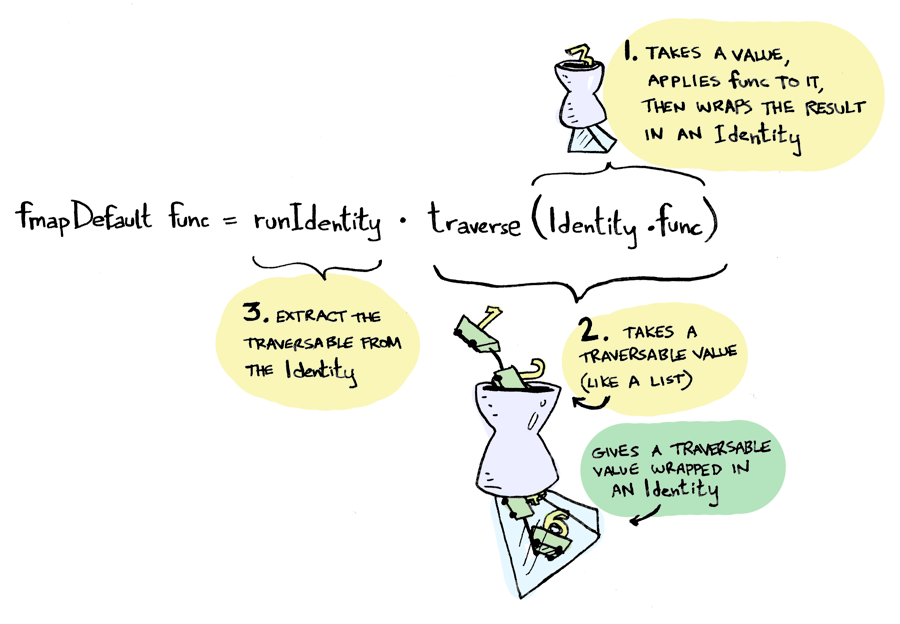
What is Identity used for? See this answer.
Using fmapDefault, let's make a function called over. over is just like fmapDefault except we pass traverse in too:
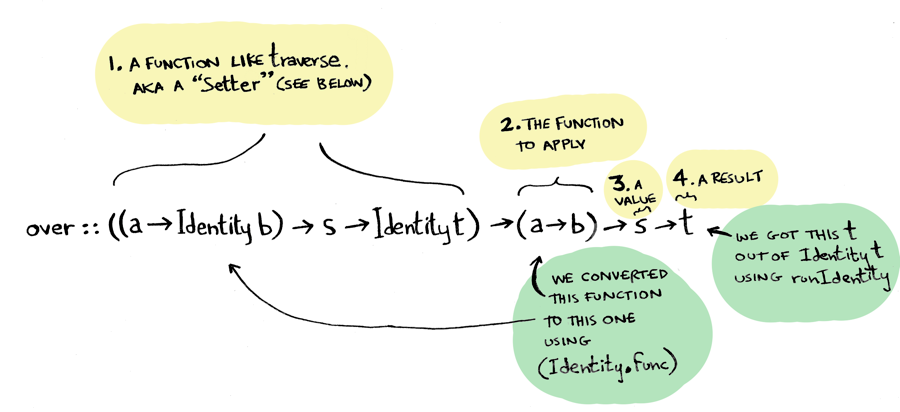
over :: ((a -> Identity b) -> s -> Identity t) -> (a -> b) -> s -> t
over l f = runIdentity . l (Identity . f)
-- over traverse f == fmapDefault f
We're so close to lenses! "Mmm I can taste the lenses Watson" drools Sherlock. "Lenses allow you to compose functors, folds and traversals together. I can feel those functors and folds mixed up in my mouth right now!"
I'll make a quick type alias here:
type Setter s t a b = (a -> Identity b) -> s -> Identity t
Now we can write over more cleanly:
over :: Setter s t a b -> (a -> b) -> s -> t
-- same as:
over :: ((a -> Identity b) -> s -> Identity t) -> (a -> b) -> s -> t
overtakes aSetter- And a transformation function
- And a value to apply it to
- Then it uses the setter to modify just a part of the value with the function.
Remember mario? Now this line makes more sense:
location.x `over` (+10) $ player1
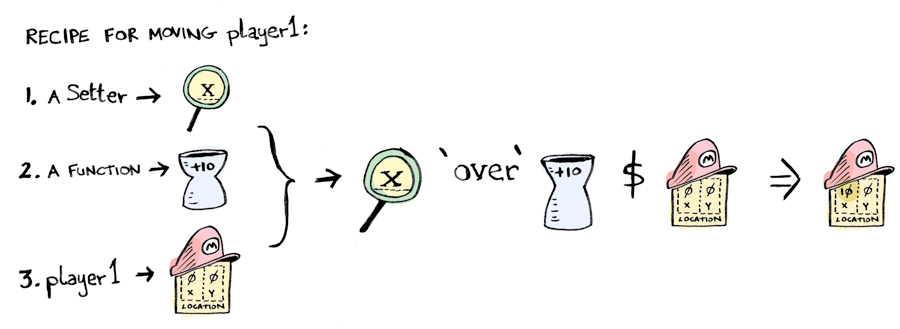
location . x is a setter. And guess what? location and x are setters too! Just like composing fmap or (.) allows you to go "one level deeper", you can compose setters and go one level deeper into your nested data! Cool!
Folds
So we are one step closer to making lenses. We just made setters, which allow us to compose functors.
Turns out, we can do the same thing for folds. First, we define foldMapDefault:
foldMapDefault :: (Traversable t, Monoid m) => (a -> m) -> t a -> m
foldMapDefault f = getConst . traverse (Const . f)
It looks very similar to our definition of fmapDefault above! We end up getting a new type alias called Fold:
type Fold s t a b = forall m. Monoid m => (a -> Const m b) -> s -> Const m t
Which looks pretty similar to a Setter:
type Setter s t a b = (a -> Identity b) -> s -> Identity t
Here's the full derivation of Fold.
Since the signatures of Fold and Setter are so similar, we should be able to combine them into one type alias. And we sure can!
type Lens s t a b = forall f. Functor f => (a -> f b) -> s -> f t

Lenses
Setters are for functors and Folds are for folds, but lenses are a more general type. They allow us to compose functors, functions, folds and traversals together! Here's an example:
Don't you hate when you fmap over a tuple, and it only affects the second part?
> fmap (+10) (1, 2)
(1,12)
What if you want it to apply to both parts? Write a lens!
> both f (a,b) = (,) <$> f a <*> f b
And use it:
> both `over` (+10) $ (1, 2)
(11,12)
And lenses can be composed to go deeper! Here we apply the function to both parts of both parts:
> (both . both) `over` (+2) $ ((1, 2), (3, 4))
((3,4),(5,6))
And we can also compose them with setters or folds!
Conclusion
Lenses can be really handy if you have a lot of nested data. Their derivation had some pretty cool parts too! Here's the full derivation.

If you liked the visual approach, check out my post on concurrency.